Calculate standard deviation effortlessly with our online Standard Deviation Calculator. Our calculator provides accurate and reliable results for statistical analysis.
Standard Deviation Calculator
Steps:
Result:
Educationise’s online standard deviation calculator is a powerful tool designed to help you easily calculate standard deviation for both population and sample data. Whether you’re a student, educator, or statistician, understanding the concept of standard deviation is essential in statistics, as it measures the spread or variability of a set of data points. This calculator not only saves you time but also provides step-by-step instructions, ensuring you understand the underlying concepts.
What is Standard Deviation?
Standard deviation (denoted as σ for population and s for sample) is a statistical measure that quantifies the amount of variation or dispersion in a data set. In simpler terms, it tells you how spread out the data points are.
- Low Standard Deviation: Data points are close to the mean (or expected value), indicating consistency in the data.
- High Standard Deviation: Data points are spread out over a wider range, indicating greater variability in the data.
The standard deviation is widely used in various fields, including finance, research, quality control, and more, to determine the reliability of data and to measure statistical error.
This calculator allows you to compute both population standard deviation and sample standard deviation, as well as confidence interval approximations, helping you make accurate statistical predictions.
How to Use Our Online Standard Deviation Calculator?
Here’s how you can find standard deviation online with our free calculator:
- Enter Your Data: Input your data points separated by commas in the provided text box.
- Choose Your Calculation Type: Select whether you are calculating for a population or a sample.
- Click “Calculate”: Hit the button to get your results and view the step-by-step calculations.
- Review the Results: The calculator will display the mean, variance, and standard deviation along with all intermediate steps.
Standard Deviation of a Population
The population standard deviation is used when you are dealing with an entire population, meaning every member of the population is measured. It is the square root of the variance of the given data set.
Formula for Population Standard Deviation:
![]()
Where:
- xi is an individual data point
- μ is the population mean (average value)
- N is the total number of values in the population
- ∑ denotes summation, meaning you add up all the values after performing the operation inside the parentheses.
Standard Deviation of a Population: Example
- Calculate the mean (μ):
- Sum all the data points and divide by the total number of values.


- Calculate the squared differences:
- Subtract the mean from each data point, then square the result.
- Example:
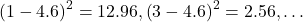
- Sum the squared differences:
- Add all the squared differences together.
- Example: 12.96+2.56+0.36+5.76+11.56=33.212.96 + 2.56 + 0.36 + 5.76 + 11.56 = 33.212.96+2.56+0.36+5.76+11.56=33.2
- Divide by the total number of values (N):
- Divide the sum of the squared differences by the total number of values (N).
- Example:

- Take the square root:
- The standard deviation is the square root of the result from the previous step.
- Example:

Thus, the population standard deviation for the data set {1, 3, 4, 7, 8} is 2.577.
Standard Deviation of a Sample
In many cases, it is not feasible to measure every member of a population. Instead, a sample is taken, and the sample standard deviation is used as an estimate of the population standard deviation. The sample standard deviation accounts for variability in a sample rather than an entire population.
Standard Deviation of a Sample Formula
![]()
Where:
- xi is an individual sample data point
- xˉ is the sample mean
- n is the sample size (number of data points)
- The term n-1 is used to correct for bias in the sample standard deviation estimate, especially for small sample sizes.
Standard Deviation of a Sample: Example
- Calculate the sample mean (xˉ):
- Sum all sample data points and divide by the sample size.
- Example:
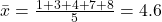
- Calculate the squared differences:
- Subtract the sample mean from each data point, then square the result.
- Example:
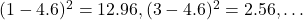
- Sum the squared differences:
- Add up all the squared differences.
- Example: 12.96+2.56+0.36+5.76+11.56=33.212.96 + 2.56 + 0.36 + 5.76 + 11.56 = 33.212.96+2.56+0.36+5.76+11.56=33.2
- Divide by n-1:
- Divide the sum of the squared differences by the sample size minus 1.
- Example:

- Take the square root:
- The sample standard deviation is the square root of the previous result.
- Example:

Thus, the sample standard deviation for the data set {1, 3, 4, 7, 8} is 2.88.
Why Use the Standard Deviation Calculator?
Our free online standard deviation calculator with steps simplifies this process by automatically computing the standard deviation for both population and sample data sets. It eliminates the need for manual calculations and ensures accurate results. Whether you need to find the standard deviation for a small sample or a large population, this tool provides the calculations with clear step-by-step instructions, making it ideal for students, teachers, and anyone interested in data analysis.
Key Features of Our Standard Deviation Calculator:
The key features of our online SD calculator are given below:
- Fast and Accurate: Provides precise calculations for both population and sample standard deviations.
- Step-by-Step Process: Shows each calculation step for better understanding.
- Easy to Use: Just enter your data set and let the calculator do the rest.
- Clear Formula Display: View the exact formulas for both population and sample standard deviation.
- Supports Multiple Data Points: Input any number of values for quick and easy calculations.
- Responsive Design: Fully optimized for all devices, ensuring a seamless user experience.
Conclusion
Understanding the Standard Deviation is essential in statistics as it provides valuable insight into data variability. Use our sd calculator to get accurate results quickly, making your statistical analysis easier and more efficient. Whether you’re working with population data or a sample, this tool will provide you with clear, step-by-step calculations, helping you better understand and interpret your data.
Frequently Asked Questions (FAQs)
1. What does a standard deviation calculator do?
A standard deviation calculator helps you measure how spread out numbers are in a dataset. It’s widely used in statistics to determine consistency and variability, whether you’re working with academic data or real-world business insights.
2. How can I find standard deviation online without doing the math manually?
You simply enter your dataset into the tool, and it instantly calculates the mean, sample deviation, and population deviation. No formulas or manual steps are needed—just accurate results in seconds.
3. Which data formats can I input into this calculator?
Whether you have whole numbers, decimals, or a long list of values, the calculator processes them efficiently. Just separate entries with commas or spaces and you’re good to go.
4. Does this calculator handle both sample and population standard deviation?
Yes, it automatically computes both. This makes it suitable for everything from school assignments to professional data reports, where understanding the difference between sample and population is crucial.
5. Why is calculating standard deviation important?
Standard deviation helps you understand how much variation exists in your data. It’s a key part of data analysis in fields like education, research, business, and quality control.
6. Is this online standard deviation tool free?
Absolutely. There are no subscriptions or sign-ups required. You can use this free tool as often as needed for assignments, presentations, or statistical evaluations.
7. Can I analyze large data sets with this calculator?
Yes, it’s designed to handle long datasets smoothly. This makes it perfect for users managing data in Excel, academic research, and business analytics.
8. Will I see how the standard deviation was calculated?
The tool provides a clear breakdown, showing you intermediate steps such as the mean and squared differences. It’s a helpful way to learn the process while checking your results.
9. How reliable is this calculator for accurate results?
The calculator uses robust statistical formulas that ensure accuracy, even for complex data. Whether you’re a student or data analyst, you can trust it to give precise outcomes.
10. Can I use this calculator for academic projects or professional reporting?
Yes, it’s built to meet both educational and professional needs. Whether you’re preparing a school report or analyzing business data, the results are reliable and easy to understand.